Les responsables ont parfois l’impression que les activités qu’ils managent ne répondent à aucune logique. Ce n’est pas souvent le cas, mais cette sensation peut résulter de plusieurs causes dont
- l’ignorance de l’existence de paramètres dont l’ influence ne peut donc être appréhendée,
- l’existence de très nombreuses variables indépendantes dont la résultante dépasse la faculté d’analyse de notre cerveau,
- le comportement imprévisible de situation pourtant parfaitement connues.
Les théories du chaos présentent des exemples de comportements parfaitement rationnels, mais dont la perception ne le parait pas.

Un problème simple : concevoir une surface finie à périmètre infini … comment oser énoncer une demande aussi inepte ? Et pourtant …
Est-ce aussi irréalisable que le "bon sens" semble le suggérer ?
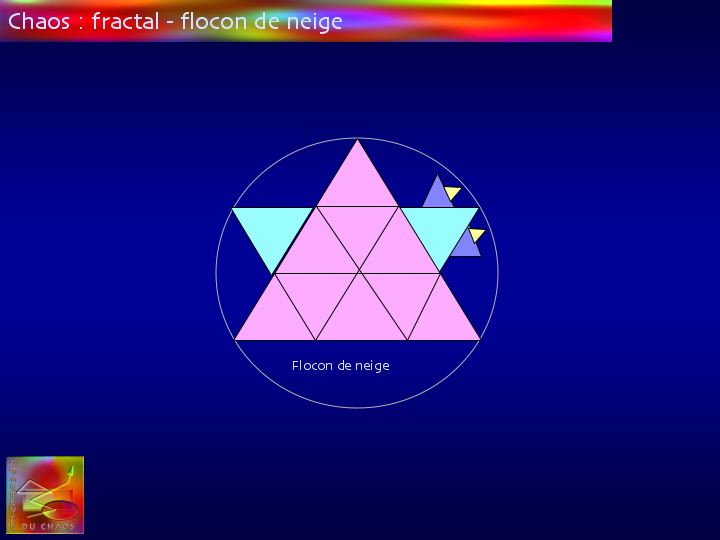
Un problème apparemment insoluble peut avoir une solution simple à la condition de faire preuve d’imagination.
Un triangle équilatéral est construit sur le tiers central du côté d'un triangle lui-même équilatéral … et ainsi de suite.
On forme ainsi une des figures fractales étudiées par Mendelbrot, appelée "flocon de neige" et conçue par von Koch.
Quelle propriété étonnante présente-t-elle ?

Cette figure simple à concevoir présente la propriété intuitivement choquante de représenter une surface finie dont le périmètre tend vers l'infinie.
On pourrait avoir l'impression d'avoir résolu l'analogue de la quadrature du cercle … sans doute pas, mais elle illustre bien la complexité de la définition de la longueur d'une côte rocheuse … sans compter l'effet des marées !
Intuitivement, on visualise bien que la multiplication de dentelures de plus en plus petite fait que le "flocon" reste cependant à l'intérieur du cercle. Sa surface reste donc finie.
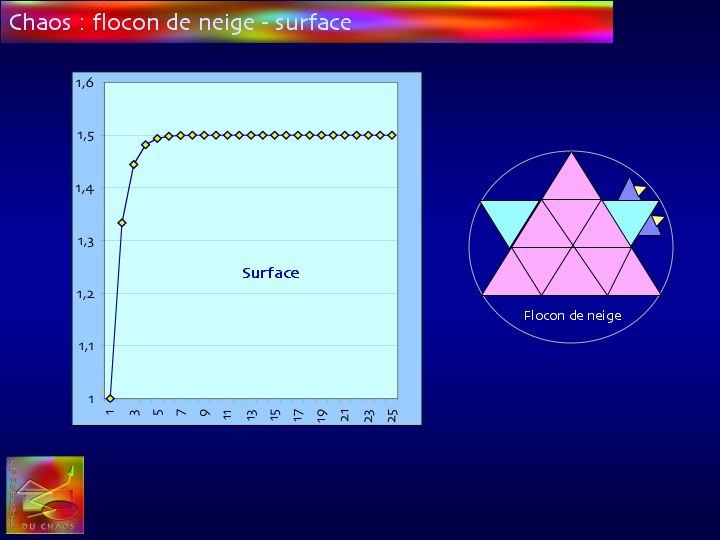
Pour ceux qui préfèrent une expression mathématique, on peut préciser qu'à chaque itération, la surface augmente du tiers de celle du triangle sur lequel les nouveaux triangles sont bâtis (les 3 premiers triangles succèdent au 9 découpés dans le triangle de départ).
La progression de la surface totale se fait donc selon les puissances de 1/3 et se calcule par : X(n+1) = Xn + [Xn + X(n-1)] / 3
La courbe ci-dessus montre l'évolution de la surface totale lorsque celle du triangle de départ est égale à 1 : elle tend vers 1,5.
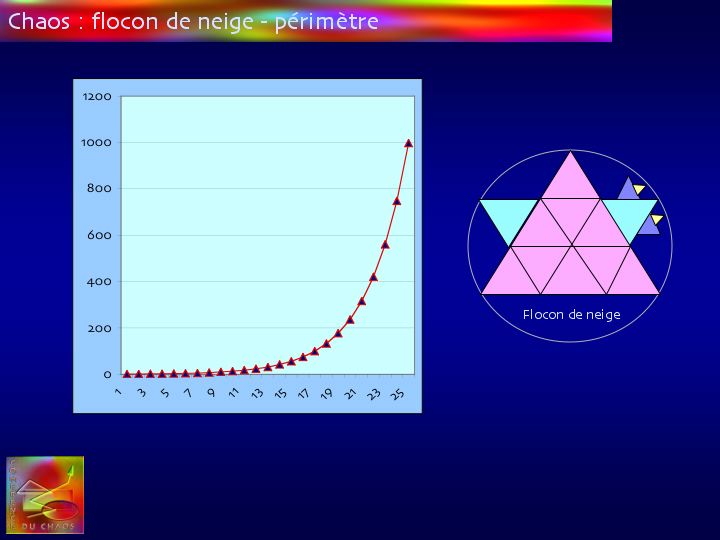
Si on cherche à calculer le périmètre, l'examen du "flocon" montre que chaque fois que l'on ampute un côté d'un triangle de son tiers, le triangle ajouté en apporte le double à la figure : c'est dire que le périmètre augmente d'un tiers à chaque opération de croissance.
A chaque itération, le nombre de segments augmente selon les puissances de 2 cependant que leur longueur décroît selon les puissances de 3.
Au total, la longueur du périmètre s'exprime par la somme :
X(n+1)=Xn*(1+Xn) : cette valeur augmente en continu avec "n" et tend vers l'infini.
Dans le même temps, la surface du flocon reste contenu dans le cercle circonscrit.

Pourquoi certaines situations sont-elles imprévisibles alors qu'elles obéissent à une loi simple ? Une des raisons possibles est l'enchaînement d'une grande série d'opérations ou les interactions d'acteurs multiples.
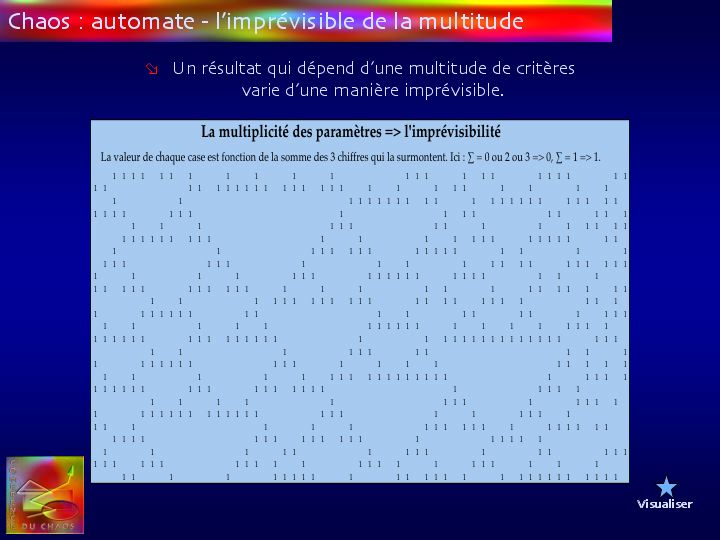
Un tel automate peut se télécharger ou se fabriquer comme suit sur un tableur :Ecrivez sur la première ligne une centaine de 1 ou de 0 (ou case vide) dans les colonnes successives d’une feuille. Par exemple de la colonne A à la colonne CP.
Choisissez librement la valeur 0 ou 1 que prendra chaque case de la ligne suivante selon que la somme des 3 cases qui la surmonte est égale à 0, 1, 2 ou 3. Par exemple = 0 si la somme est inférieure à 3 et 1 si elle atteint cette valeur.
Dans l'hypothèse ci-dessus, programmez la case la plus à gauche (colonne A) de la ligne N°2 avec la formule suivante :=SI(CP1+A1+B1=0;0;SI(CP1+A1+B1=1;1;SI(CP1+A1+B1=2;0;SI(CP1+A1+B1=3;0;1))))Dans la colonne B de la même ligne 2 placer la formule :=SI(A1+B1+C1=0;0;SI(A1+B1+C1 =1;1;SI(A1+B1+C1 =2;0;SI(A1+B1+C1 =3;0;1))))Copier à droite cette formule jusqu’à la colonne CO incluse
Dans la case suivante (CP2), pour obtenir un automate circulaire, la formule est :=SI(CO1+CP1+A1=0;0;SI(CO1+CP1+A1 =1;1;SI(CO1+CP1+A1 =2;0;SI(CO1+CP1+A1 =3;0;1))))Copier la totalité de cette ligne 2 vers le bas jusqu'à, par exemple, la ligne 100
Votre modèle est prêt : enregistrez-leModifiez la valeur 1 ou 0 (“rien”) d’une des cases de la ligne 1 et observez ce qui se passe : une perturbation se propage vers le bas et progressivement en largeur. On obtient une nouvelle apparence pseudo-régulière, mais il est pratiquement impossible de prévoir si la valeur d’une case donnée de la ligne 100 sera modifiée ou non.
On est en présence d'un résultat imprévisible, intuitivement bien que déterministe : seul le calcul peut apporter la réponse ... même s'il est vrai que vous n'avez qu'une chance sur deux de vous tromper !
A noter que l’ensemble des lignes et colonnes qui ne présente pas un aspect anarchique, mais garde un aspect général, ordonné, pseudo-régulier, est typique d'une propriété que l'on constate souvent dans les systèmes complexes : ils ont tendance à s'auto-organiser.Dans le management, on a souvent à prendre en compte de nombreux paramètres qui génèrent une imprévisibilité d'autant plus grande que, contrairement au cas de l'automate ci-contre, on ne connaît pas les règles d'interaction entre les éléments. Il ne faut pas chercher à tout organiser dans tous les détails, mais faire confiance à une certaine aptitude de l'ensemble à trouver une solution inédite à un problème nouveau.
>Pour s'amuser un peu : remplacez la première ligne de votre tableur par la séquence suivante :
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Changez-le "1 orange" en "0". Vous avez l'impression que rien n'a changé ... vous avez raison : la modification d'un chiffre de la première rangée n'entraîne pas forcément un bouleversement de l'ensemble.
Puisse cet exercice vous rendre plus attentif au comportement souvent imprévisible des systèmes complexes ...