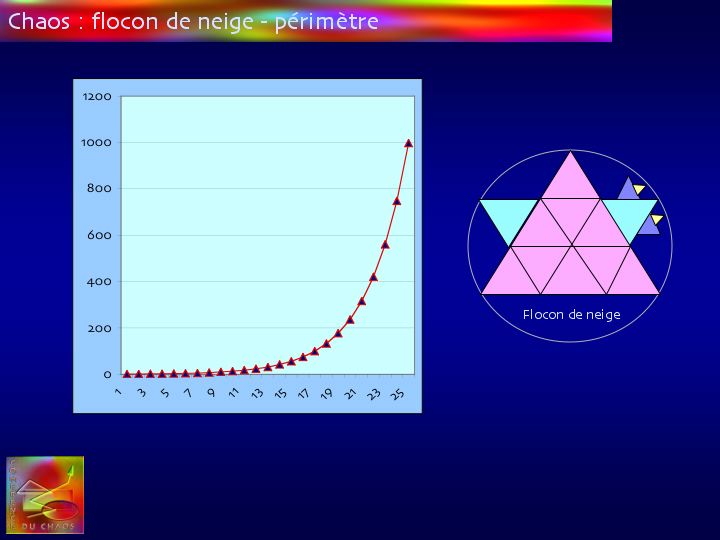
Si on cherche à calculer le périmètre, l'examen du "flocon" montre que chaque fois que l'on ampute un côté d'un triangle de son tiers, le triangle ajouté en apporte le double à la figure : c'est dire que le périmètre augmente d'un tiers à chaque opération de croissance.

A chaque itération, le nombre de segments augmente selon les puissances de 2 cependant que leur longueur décroît selon les puissances de 3.

Au total, la longueur du périmètre s'exprime par la somme :

X(n+1)=Xn*(1+Xn) : cette valeur augmente en continu avec "n" et tend vers l'infini.

Dans le même temps, la surface du flocon reste contenu dans le cercle circonscrit.