Il ne s’agit pas ici de parler de transport, approvisionnement ou supply chain, mais d’une équation mathématique connue sous ce nom … pour je ne sais plus quelle raison.
Sous les apparences d’une formule très simple elle a de quoi surprendre un technicien qui manquerait de fantaisie ou … d’ouverture d’esprit, mais regardons cela de plus près.
Il s'agit d'une série mathématique très simple dont le comportement varie énormément et d'une manière surprenante en faisant varier un paramètre d'apparence bénigne.
Pour certaines grandeurs, son évolution devient totalement imprévisible : de quoi surprendre plus d'un esprit logique.
Au départ l’équation logistique a été conçue comme représentative de l’évolution d’une population sur un territoire limité : tant qu’il y a de l’espace disponible son nombre croît en fonction du nombre existant - k * X(n) - mais il faut un facteur limitation de la croissance pour ne pas dépasser les possibilités nutritives du terrain cultivable soit k * {1 - X(n)}.
Cette équation est très simple et pourtant son comportement est surprenant.
Un document réalisé sur un tableur et intitulé "Equation logistique" permet de tester des variantes de "k" et de "X(1). Seules leurs cases de la page "k=2" ne sont pas verrouillées. Il est téléchargeable.
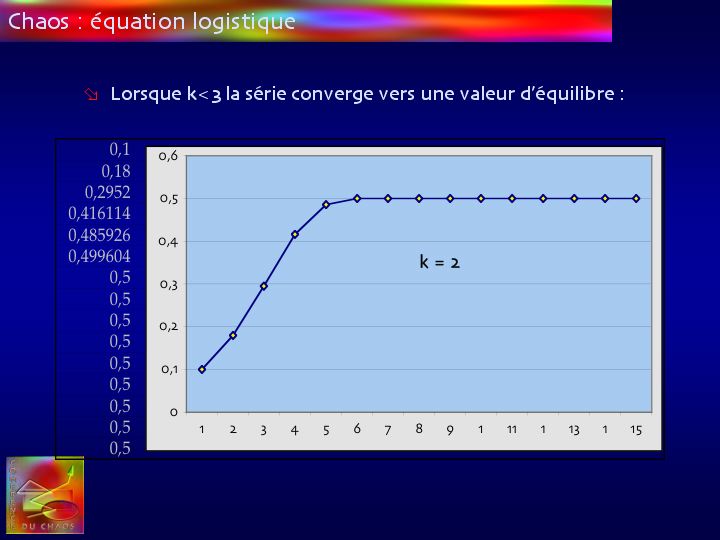
Instinctivement, on comprend que, pour la valeur de k=2, la population va croître puisqu’elle a tendance à doubler la génération précédente avec un freinage imposé par le deuxième terme de l’équation.
Le nombre d’individus va se stabiliser progressivement à un nombre correspondant à la consommation de la totalité des ressources disponibles tout en satisfaisant les besoins de chaque individu.
Il n'y a rien là de surprenant. Mais que se passe-t-il si on change la valeur de k ?
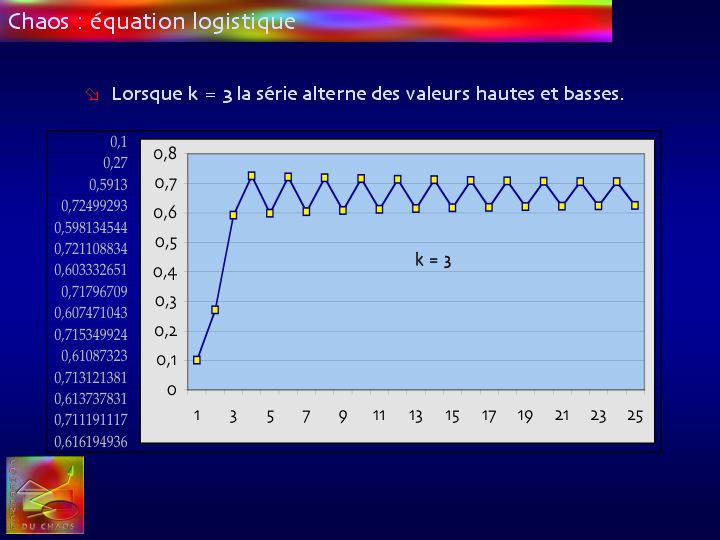
D’une manière un peu étonnante, la population augmente au-delà du point d’équilibre puis oscille autour de ce dernier en convergent lentement, mais cela est analogue au phénomène de pompage qui est bien connu en physique.
C'est déjà un comportement plus inhabituel, mais qui n'est pas trop surprenant pour les physiciens sinon pour le commun des mortels.
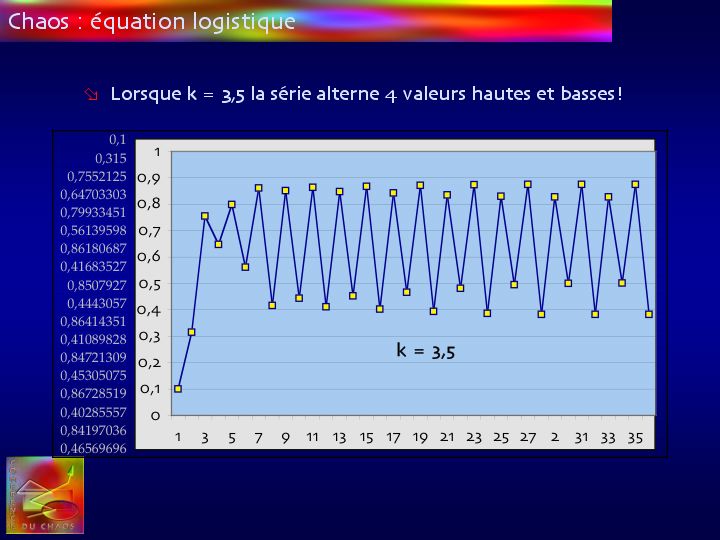Avec ces paramètres, le modèle se stabilise, d’une manière beaucoup moins évidente, sur 4 valeurs différentes. Le chiffre suivant reste cependant devinable - ici un peu au-dessus de 0,8 - puisqu’ils alternent régulièrement.
Changeons encore la valeur de k de cette même équation qui paraissait simpliste.
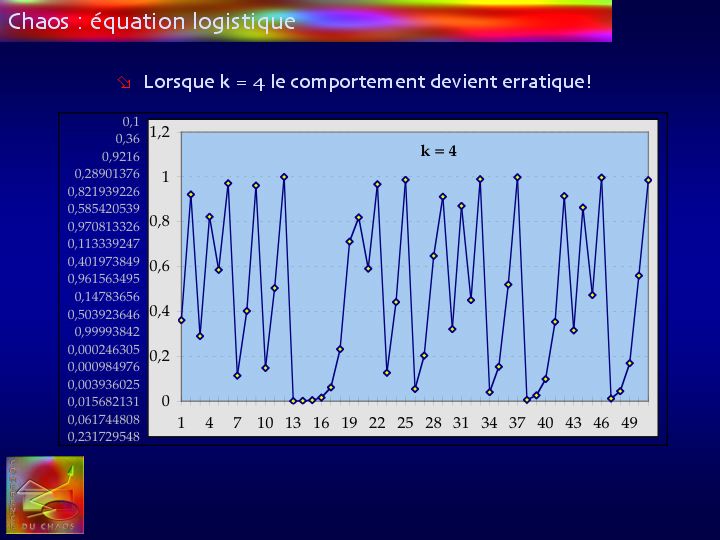
En gardant toujours la même valeur initiale de 0,1, mais en retenant 4 pour le coefficient k, les points successifs de la courbe fluctuent entre les valeurs extrêmes possibles - 0 et 1 - d’une manière qui paraît totalement erratique. La connaissance des valeurs précédentes ne permet plus du tout d’anticiper l’ordre de grandeur de la suivante.
Au vu du graphique, le régime est devenu imprédictible alors qu’il s’agit du résultat d’un calcul très simple et que la valeur suivante est totalement déterminée, mais imprévisible sans recourir au calcul.
Ici le bon sens est pris en défaut !
>
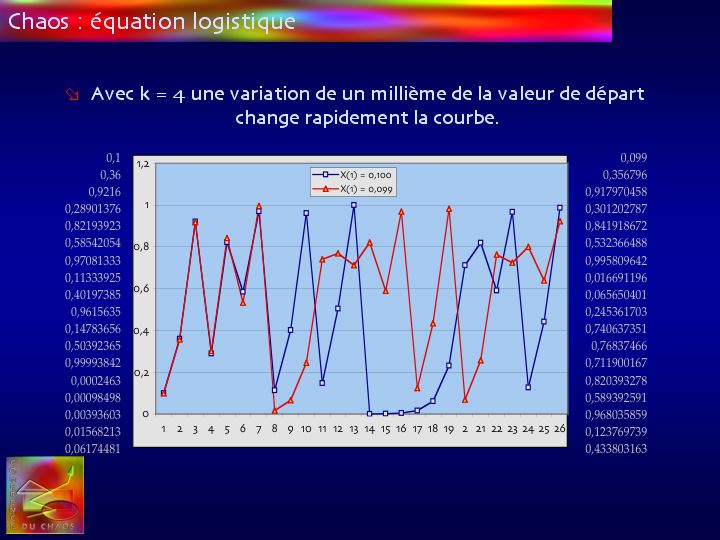
Une autre propriété de cette équation est surprenante même si a posteriori, elle est explicable.
Une variation infime des conditions initiales - la valeur de x(1) - n’entraîne, au départ, aucune variation significative, mais rapidement les courbes divergent fortement.
Ce comportement s’explique par le caractère exponentiel de l’écart entre les deux formules.
En management, par analogie, une décision de second ordre peut aussi bien conduire l’activité à la catastrophe qu’au succès … De ce point de vue, on pourrait considérer que le patron d'un grand groupe de 100 000 personnes ne peut avoir qu'une influence marginale et que le destin de l'entreprise ne dépend au fond pas beaucoup de lui. Et pourtant, s'il est vrai que, à court terme, l'entreprise semble avancer sur sa lancée, au bout de quelques années, elle peut dériver gravement : des exemples comme Elf Aquitaine, Vivendi, Rhodia ou Alstom me paraissent des illustrations qui se passent de commentaires.
Il est clair aussi que cet avenir bien que parfaitement déterministe et apparemment imprévisible … pour tous ceux qui n'auront pas réussi à trouver l'algorithme qui permet de calculer la valeur du point suivant … d'où l'importance de réussir à comprendre les forces qui font évoluer une activité.
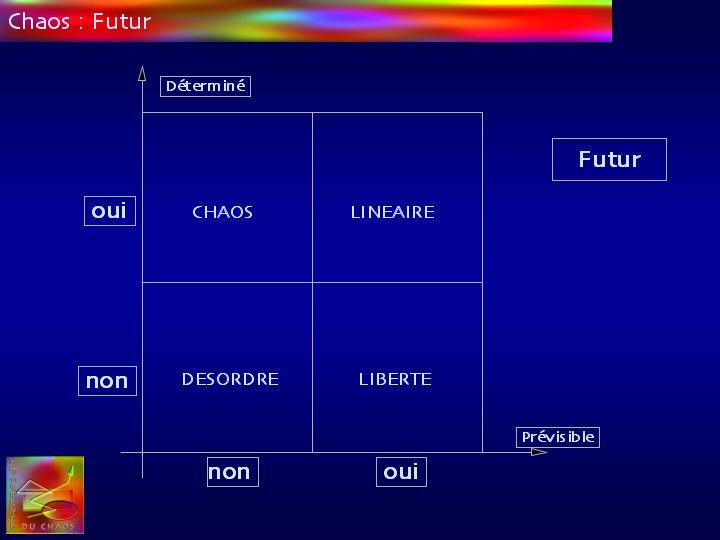
On peut, en tirant leçon de l'équation logistique, définir quatre types d'avenir
LINEAIRE : Avenir déterminé et prévisible
=> liberté nulle
CHAOS : Avenir déterminé mais imprévisible
=> liberté illusoire
DESORDRE : Avenir indéterminé et imprévisible
=> liberté apparente
LIBERTE : Avenir indéterminé mais voulu
=> liberté exprimée
Tout manager doit s'attendre à rencontrer ces diverses situations :
la linéaire, valable pendant les 30 glorieuses ou lorsque la demande était en croissance régulière et forte, est confortable, mais ne permet guère de faire mieux que ses concurrents … sauf s'ils ne sont pas conscients.
- Le chaos est souvent confondu avec le désordre, car on n'y comprend rien, et pourtant, si l'on est dans une situation chaotique, celui qui arrivera à trouver l'équation simple expliquant un comportement apparemment erratique, deviendra capable de prévoir l'avenir et d'agir en conséquence.
- Le désordre me paraît être fréquemment le domaine de la politique parce que le grand nombre d'avis individuels (dans un pays démocratique !) rend impossible l'anticipation de la résultante tant des événements objectivement d'importance secondaire peuvent faire basculer une majorité et que dans le même temps l'expression de la liberté individuelle est réelle.
- La dernière se rencontre assez fréquemment dans les entreprises, car si l'avenir d'une activité est bien fonction des libres choix de ses acteurs clés, ceux-ci ne sont souvent pas si nombreux que l'on ne puisse en avoir une connaissance assez précise pour être capable d'anticiper leurs choix.
La complexité entraîne l’incertitude. Ce qui ne veut pas dire insécurité ou liberté totale.
