
Un problème simple : concevoir une surface finie à périmètre infini … comment oser énoncer une demande aussi inepte ? Et pourtant …
Est-ce aussi irréalisable que le "bon sens" semble le suggérer ?
Un problème apparemment insoluble peut avoir une solution simple à la condition de faire preuve d’imagination.
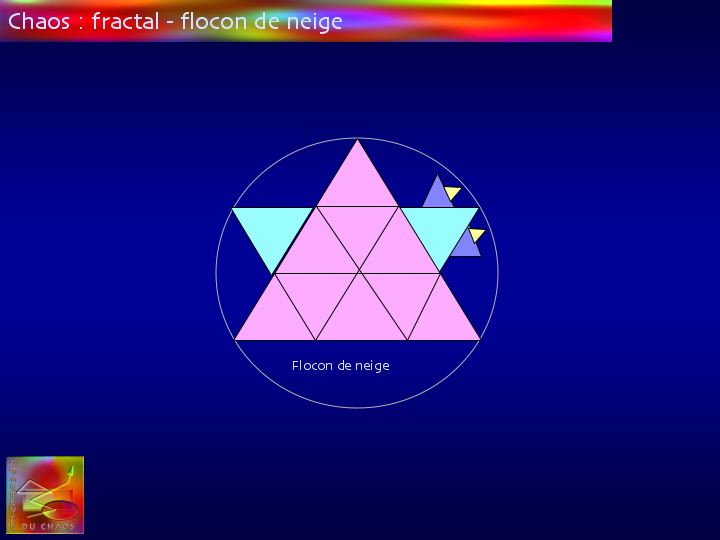
Un triangle équilatéral est construit sur le tiers central du côté d'un triangle lui-même équilatéral … et ainsi de suite.
On forme ainsi une des figures fractales étudiées par Mendelbrot, appelée "flocon de neige" et conçue par von Koch.
Quelle propriété étonnante présente-t-elle ?

Cette figure simple à concevoir présente la propriété intuitivement choquante de représenter une surface finie dont le périmètre tend vers l'infinie.
On pourrait avoir l'impression d'avoir résolu l'analogue de la quadrature du cercle … sans doute pas, mais elle illustre bien la complexité de la définition de la longueur d'une côte rocheuse … sans compter l'effet des marées !
Intuitivement, on visualise bien que la multiplication de dentelures de plus en plus petite fait que le "flocon" reste cependant à l'intérieur du cercle. Sa surface reste donc finie.
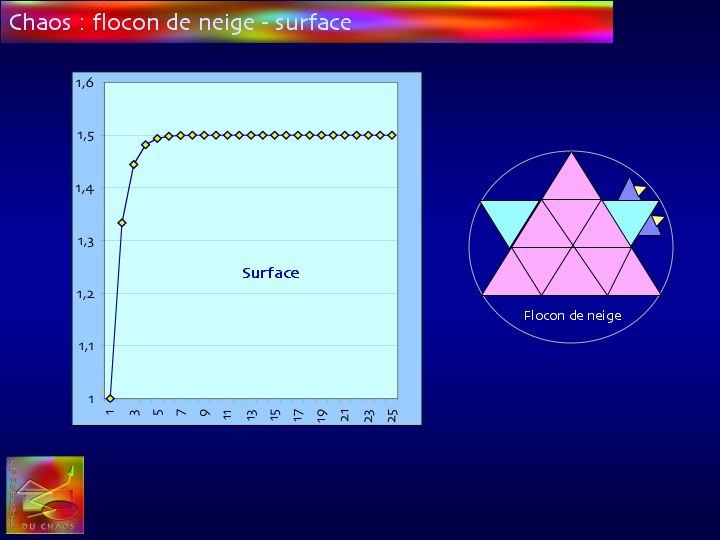
Pour ceux qui préfèrent une expression mathématique, on peut préciser qu'à chaque itération, la surface augmente du tiers de celle du triangle sur lequel les nouveaux triangles sont bâtis (les 3 premiers triangles succèdent au 9 découpés dans le triangle de départ).
La progression de la surface totale se fait donc selon les puissances de 1/3 et se calcule par : X(n+1) = Xn + [Xn + X(n-1)] / 3
La courbe ci-dessus montre l'évolution de la surface totale lorsque celle du triangle de départ est égale à 1 : elle tend vers 1,5.
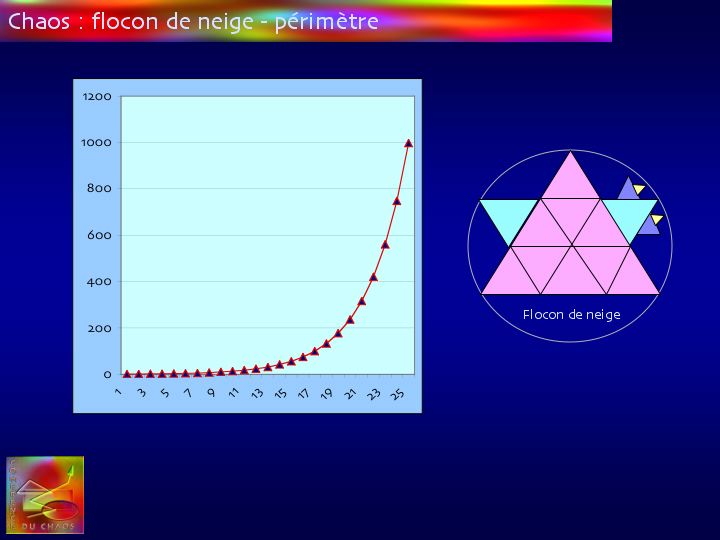
Si on cherche à calculer le périmètre, l'examen du "flocon" montre que chaque fois que l'on ampute un côté d'un triangle de son tiers, le triangle ajouté en apporte le double à la figure : c'est dire que le périmètre augmente d'un tiers à chaque opération de croissance.
A chaque itération, le nombre de segments augmente selon les puissances de 2 cependant que leur longueur décroît selon les puissances de 3.
Au total, la longueur du périmètre s'exprime par la somme :
X(n+1)=Xn*(1+Xn) : cette valeur augmente en continu avec "n" et tend vers l'infini.
Dans le même temps, la surface du flocon reste contenu dans le cercle circonscrit.

