Il ne s’agit pas ici de parler de transport, approvisionnement ou supply chain, mais d’une équation mathématique connue sous ce nom … pour je ne sais plus quelle raison.
Sous les apparences d’une formule très simple elle a de quoi surprendre un technicien qui manquerait de fantaisie ou … d’ouverture d’esprit, mais regardons cela de plus près.
Il s'agit d'une série mathématique très simple dont le comportement varie énormément et d'une manière surprenante en faisant varier un paramètre d'apparence bénigne.
Pour certaines grandeurs, son évolution devient totalement imprévisible : de quoi surprendre plus d'un esprit logique.
Au départ l’équation logistique a été conçue comme représentative de l’évolution d’une population sur un territoire limité : tant qu’il y a de l’espace disponible son nombre croît en fonction du nombre existant - k * X(n) - mais il faut un facteur limitation de la croissance pour ne pas dépasser les possibilités nutritives du terrain cultivable soit k * {1 - X(n)}.
Cette équation est très simple et pourtant son comportement est surprenant.
Un document réalisé sur un tableur et intitulé "Equation logistique" permet de tester des variantes de "k" et de "X(1). Seules leurs cases de la page "k=2" ne sont pas verrouillées. Il est téléchargeable.
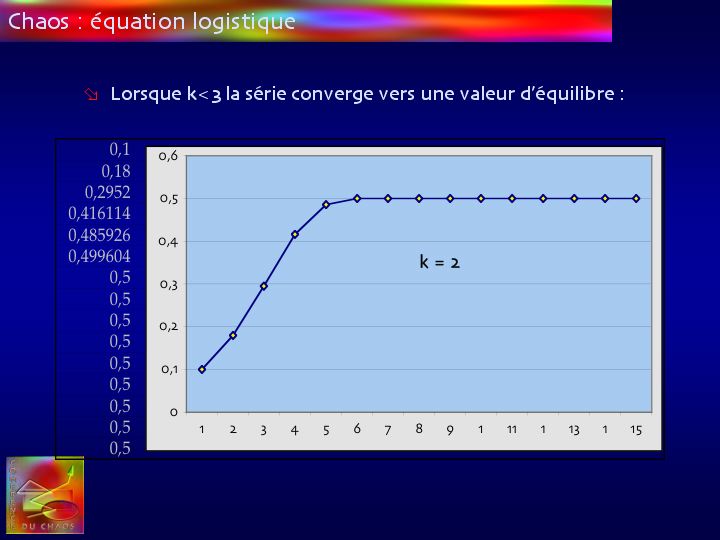
Instinctivement, on comprend que, pour la valeur de k=2, la population va croître puisqu’elle a tendance à doubler la génération précédente avec un freinage imposé par le deuxième terme de l’équation.
Le nombre d’individus va se stabiliser progressivement à un nombre correspondant à la consommation de la totalité des ressources disponibles tout en satisfaisant les besoins de chaque individu.
Il n'y a rien là de surprenant. Mais que se passe-t-il si on change la valeur de k ?
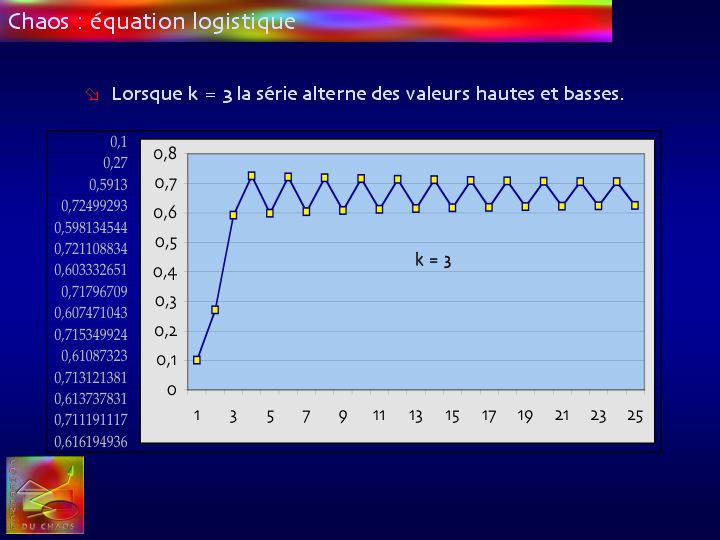
D’une manière un peu étonnante, la population augmente au-delà du point d’équilibre puis oscille autour de ce dernier en convergent lentement, mais cela est analogue au phénomène de pompage qui est bien connu en physique.
C'est déjà un comportement plus inhabituel, mais qui n'est pas trop surprenant pour les physiciens sinon pour le commun des mortels.
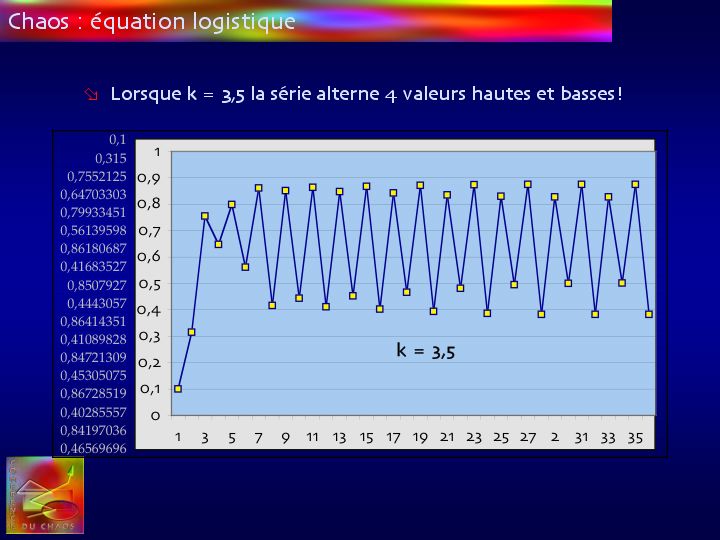Avec ces paramètres, le modèle se stabilise, d’une manière beaucoup moins évidente, sur 4 valeurs différentes. Le chiffre suivant reste cependant devinable - ici un peu au-dessus de 0,8 - puisqu’ils alternent régulièrement.
Changeons encore la valeur de k de cette même équation qui paraissait simpliste.
